Notes on the Theory of Urban Residential Structure:
The Basic Urban Model
Professor Yinger
Exercises
Part I. Bid Functions and Density Functions
- The slope of the bid-price function, P {u}, is –t/H. Use Equation (35) to derive general expression for the slope of the bid-rent function, R {u}.
- Derive expressions for the slopes of the bid-rent function, R{u}, and the population density function, D{u}, in the case of a Cobb-Douglas utility function.
- Equation (48) provides an expression for the population function N{u} with a Cobb-Douglas utility function. Derive and explain the slope of this function.
- Derive an expression for the second derivative of the bid-price function, P{u}, with a Cobb-Douglas utility function.
- Derive expressions for the second derivatives of the bid-rent function, R{u}, and the population density function, D{u}, in the case of a Cobb-Douglas utility function.
Part II. Comparative Statics
- Derive expressions for the comparative static derivatives dP{u}/dα and dP{u}/da in a basic open urban model and determine their signs.
- Prove that the closed-model comparative static derivative dR{u}/d , which is given by Equation (64), is positive.
- Derive an expression for the comparative static derivative d /dY in a basic closed urban model. Prove that this derivative is positive. [Hint: One possible approach is to use Equations (40) and (55) to show that if d /dY is negative, dD{u}/dY also must be negative, which is a contradiction; if both density and the size of the urban area increase, population cannot remain constant.]
- Prove that with Cobb-Douglas utility and housing production functions,
(a) in an open urban model, dR{u}/dt < 0;(b) in a closed urban model, dR{u}/dt > 0 for u < u* and dR{u}/dt < 0 for u > u*, where 0 < u* < .[Hint: Use the population integral.]
10. Derive and evaluate the signs of expressions for the following comparative static derivatives in a basic open urban model with Cobb-Douglas utility and housing production functions: d /dY, d /dt, d /dU*, d /d , dR{u}/dY, dN/dY, and dR{u}/d .
11. Derive and evaluate the signs of expressions for the following comparative static derivatives in a basic closed urban model with Cobb-Douglas utility and housing production functions: d /dY, d /d , and dR{u}/d .
Part III. Bid Functions with Alternative Utility Functions
- Derive bid-price and bid-rent functions for a basic urban model with a utility function of the following form:where the α=s, β, and ω are constants. Express the bids either as functions of U*, the fixed utility level, or , the outer edge of the urban area. Assume that the housing production function is Cobb-Douglas. For extra credit, derive the population integral.
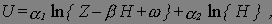
where the α=s, β, and ω are constants. Express the bids either as functions of U*, the fixed utility level, or , the outer edge of the urban area. Assume that the housing production function is Cobb-Douglas. For extra credit, derive the population integral.
Solve an urban model with a CES utility function. Specifically,
(a) Derive a price-distance function when households have a CES utility function (and all other assumptions for a basic urban model hold). [Hint: Remember that the answer is not altered by a monotonic transformation of the utility function; a CES utility function, unlike a CES production function, does not need the “outer” exponent.]
(b) Derive the corresponding rent-distance function (assuming Cobb-Douglas housing supply).
(c)Derive the population integral for this case (but you do not need to integrate it).
- Assume that leisure time, S, is an argument in a household’s utility function, that the utility function is Cobb-Douglas, and that total time available, T, must equal work time, W, plus S plus time spent commuting, which is u/M, where M is commuting speed (miles per hour). In addition, assume that the round-trip operating costs of commuting equal t0 per mile. Derive a bid-price function based on these assumptions. Compare it to the bid-price function derived in the text.
Part IV. Alternative Urban Models
- All workers in Bigtwo have identical Cobb-Douglas utility functions and identical skills. Bigtwo has only two employers, each of which is located in the CBD and each of which provides free buses to its employees. Firm A provides fancy buses with a smooth, quiet ride and with many forms of entertainment, such as movies, television, computers, and music. Firm B provides ordinary buses, which are not so smooth and quiet and which provide no entertainment at all.Workers are perfectly mobile, so they must obtain the same utility level, regardless of where they work. You have observed that employees of both firms live in neighborhoods located exactly u* miles from the CBD.(a) Which group of workers, employees of firm A or firm B, live outside u*?(b) Which group of workers has higher wages? How much higher?
- Naderville has a greenbelt, that is, a wooded park, on a ridge that runs in a circle around the CBD. The distance between the CBD and the greenbelt is u* miles. All residents of Naderville have the same incomes, utility functions, and commuting costs. Moreover, they are all very proud of the greenbelt and like to look at it. In fact, residents of Naderville are willing to pay for a better view of the greenbelt from their home. The quality of this view declines with distance from the greenbelt.More specifically, each resident of Naderville has the following utility function:
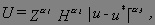
where all the α=s are positive and α1 + α2 = 1.
(a) Derive the price-distance function for Naderville, expressed as a function either of the fixed utility level, U*, or of the outer edge of the urban area, .
(b) Derive the condition under which the price-distance function in Naderville will be positively sloped for locations inside u*.
- Write down a standard urban model with Cobb-Douglas utility and production functions and two income classes. Assume that these two classes have the same utility functions and that commuting costs consist of time costs, which are proportional to income, and on operating costs, which are the same for both groups.(a) The bid functions of the two groups cross at distance u* from the CBD. Prove that the higher-income class lives outside u*.(b) Derive an expression for the population in each group.(c) Suppose operating costs are also proportional to income. Does this affect your answer to part (a)? Explain.
- Derive the so-called land constant for an urban model with a street grid and any pattern of arteries that is not considered in “Around the Block.” For example, you could consider vertical and horizontal arteries through the CBD and two vertical arteries that do not go through the CBD.
- The country of Equalomia is dedicated to equality. The economy of Equalomia is based on free enterprise, subject to various rules designed to make market outcomes more equal. In recognition of the need for work incentives, the government does not insist on complete equality, and households in Equalomia fall into one of two income classes, which both contain the same number of people. Households in the richer income class earn exactly twice as much as households in the poorer class. The government has been unwilling to diverge from complete equality in the housing market, however, and every household in Equalomia receives exactly kY* units of housing services, where k is a constant set by the government and Y* is average household income. Thus, households can compete with each other for existing apartments, but all apartments contain kY* units of housing services.Your job is to describe urban structure in Equalomia. You have discovered that everyone works in the city center; that per-mile commuting costs are constant within an income class; that household’s have Cobb-Douglas utility functions; that housing services are produced with a fixed coefficients production function using land and capital (that is, HS{u} = aL{u} = bK{u}, where HS{u} is total housing services supplied at distance u and a and b are constants); and that the amount of residential land is proportional to distance (that is, L{u} = φu, where φ is a constant).
